一、电感的单位
从上一篇可知,电感反映的是一种器件对抗电流变化的能力。这种“对抗”体现在电感上产生了感应电流和感应电动势(也叫:反向电动势,Back EMF)。
电感的单位是Henry,符号是L。L=1 Henry的定义是:电流以每秒钟1安培的节奏变化(1A/s),如果在电感上产生的感应电动势的电压是1V,这种电感就是1 Henry。
在无线电和通信设备中,常见的电感单位是nH(纳亨),应对MHz级别的电流变化;在电源和供电设备中,常见的电感单位是μH(uH,微亨),应对KHz级别的电流变化;在音频设备中,常见的电感单位是mH(豪亨),应对数百Hz~2KHz级别的电流变化。
电感在对抗电流变化的过程中,伴随着电能和磁能的转化,电感的容量越大,所能转化和储存的能量也越大。
二、电感上的电压、电流变化
我们来看一下电感上的电压和电流的关系公式:V=-L*di/dt
该公式反映了电感上感应电动势的电压大小和电流变化快慢有关。
在L恒定的情况下,电流变化越快,产生的感应电动势电压越高。特别是在电路开关断开或闭合的时候,电流的瞬间变化,可以使得在电路开关的地方出现火花(把空气击穿才能产生火花,至少是上万伏的电压,瞬间电压很高,持续时间短,但能量不一定大)。
我们构建一个电感、电阻、电源(周期性方波)组成的电路,如下所示:
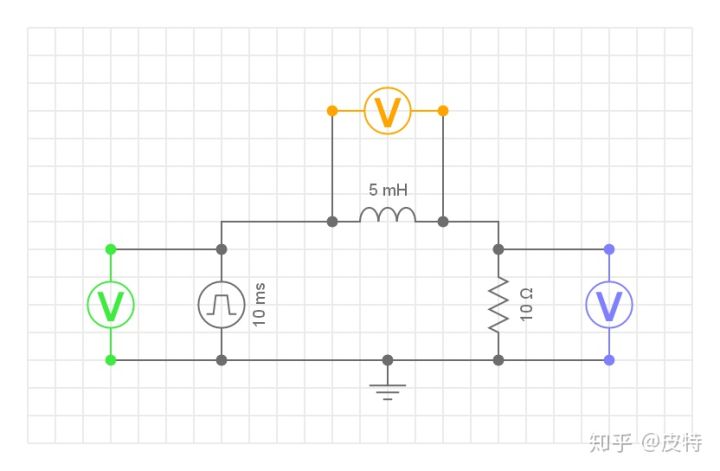
每个器件上都并联了电压表,便于查看波形。特别的,通过电阻上的电压,可以推测整个电路上的电流(欧姆定律)。电源采用的是Max 10V,Min 0V,100Hz的周期性方波。
我们来看一下电感上电压、电流波形变化:
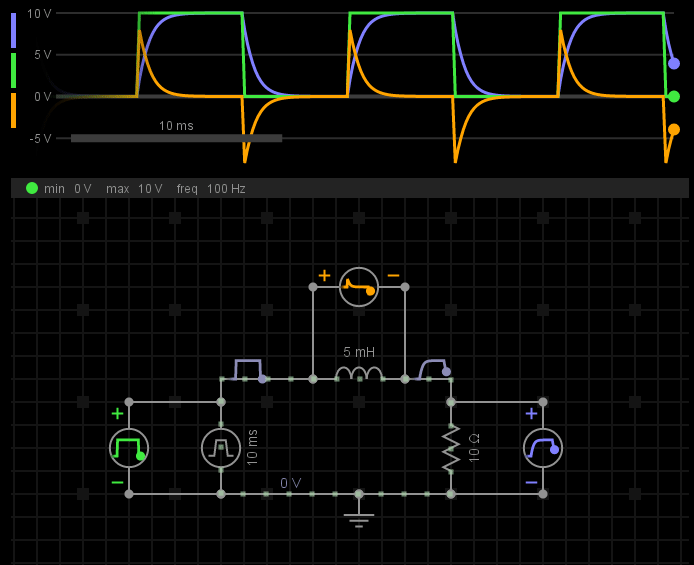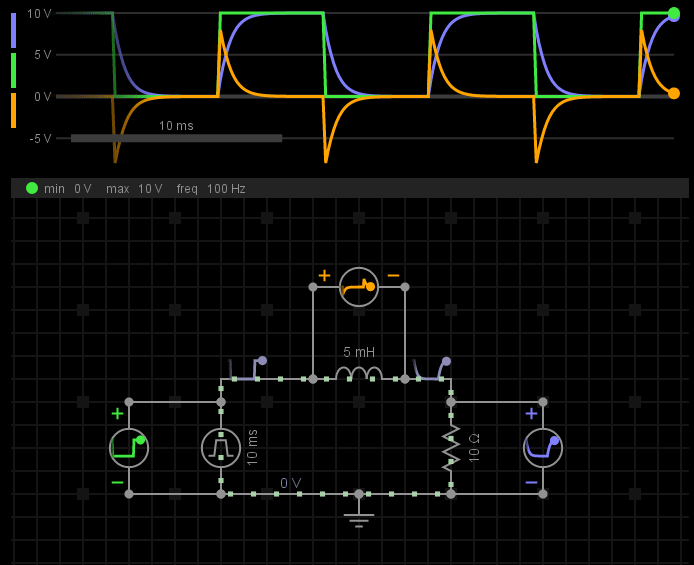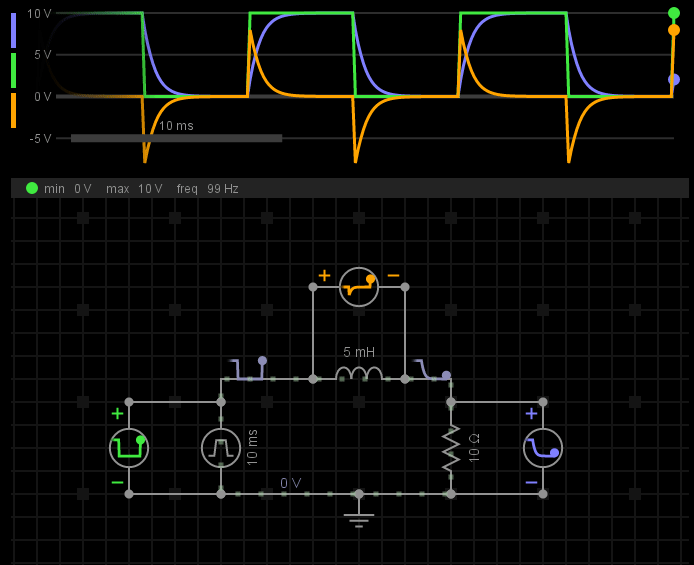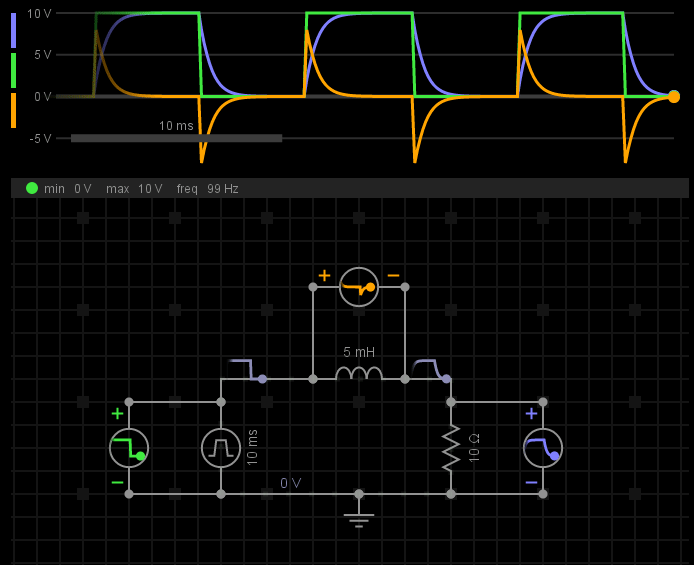
其中,绿色波形表示电源电压变化;黄色波形表示电感电压变化;蓝色波形表示电阻电压变化,也反映了整个电路上的电流变化。
当电源从0V->10V变化时,电感的电压产生一个正脉冲(电压突变),这个脉冲极性与电源电压极性相反。由于电感电压削弱了电源电压的影响,所以电流没有突然变大,整个电路的电流从0A开始,逐渐上升(电流不能突变),直至达到稳态。
当电源从10V->0V变化时,电感的电压产生一个负脉冲(电压突变),这个脉冲极性与电源电压极性相同。由于电感电压延续了电源电压的影响,所以电流没有突然变小,整个电路的电流从1A(10V/10Ω)开始,逐渐下降(电流不能突变),直至达到稳态。
这和我们上一篇说的,电感是电磁学领域中的惯性器件是一致的,它不喜欢电流发生改变,总是利用自己的能量维持电流原本的状态。
注意,这个电路里面特意没有放置开关器件,即使电源电压最小是0V的时候,整个电路也是导通的。但如果放一个开关在电路里,开关断开的情况和电源是0V的情况表现是不一样的,我们后续再分析。你可以想象一下,电感作为电流的惯性器件,如果电路突然断开,电流没有回路,会发生什么?
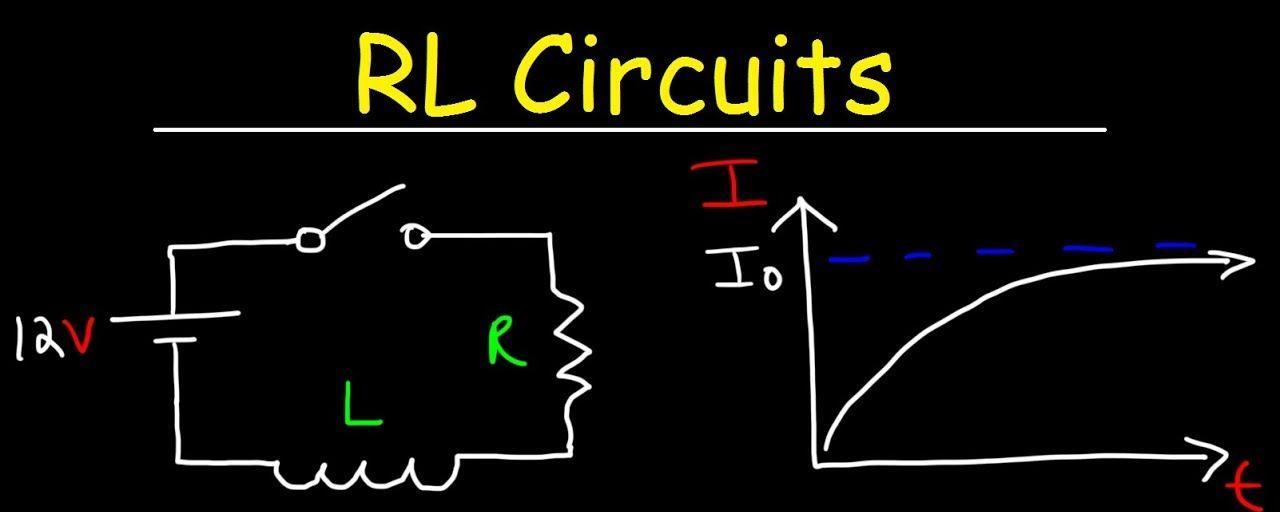
三、电感的时间常数
LR电路中,应对外部激励(直流)变化,电感的电压和电流达到稳定状态需要一定的过程,其波形符合指数变化:
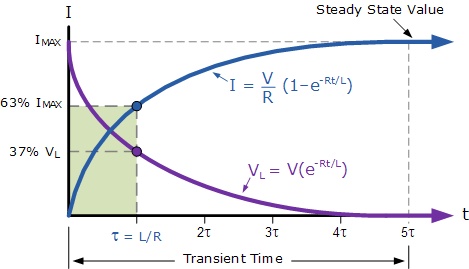
图3-电感的电压和电流变化曲线(直流激励下)
时间常数τ=L/R。经历5个τ后,电感的电压和电流趋于稳定,特别对于直流来说,此时电感相当于短路,电流达到最大Imax=V/R。
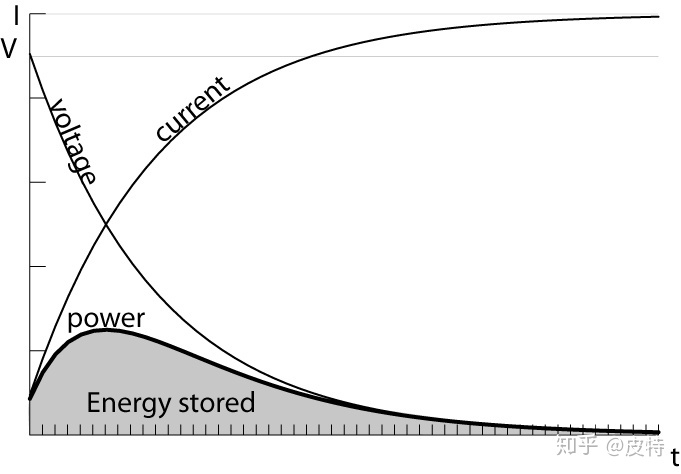
图4-电感储存的能量(V*I的积分)
在达到稳态的过程中,电感也在储存能量(将电能转化为磁能,对应上述激励电源从0V->10V变化的情况)或者释放能量(将磁能转化为电能,对应上述激励电源从10V->0V变化的情况)。所以该常数也称为充放电时间常数。
四、电感的阻抗——感抗
与电容一样,衡量不同频率激励下的电感表现需要用到阻抗,特别的,对于纯电感电路,阻抗就是感抗。
计算电感感抗的公式是X=2π*f*L。频率越高,感抗越大。
譬如,我们将图2中的电源激励,从100Hz增大到1KHz,会发生什么?
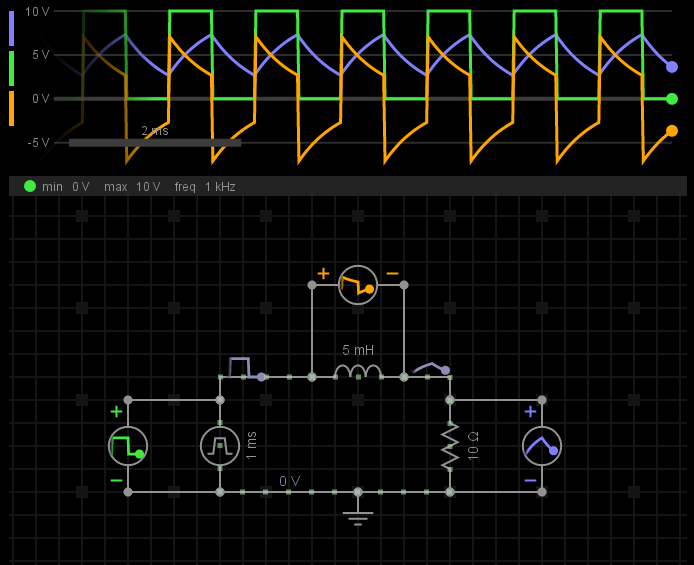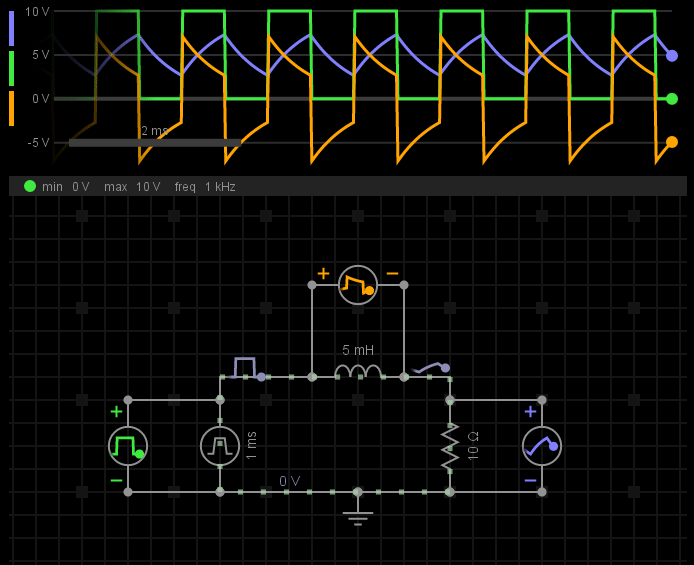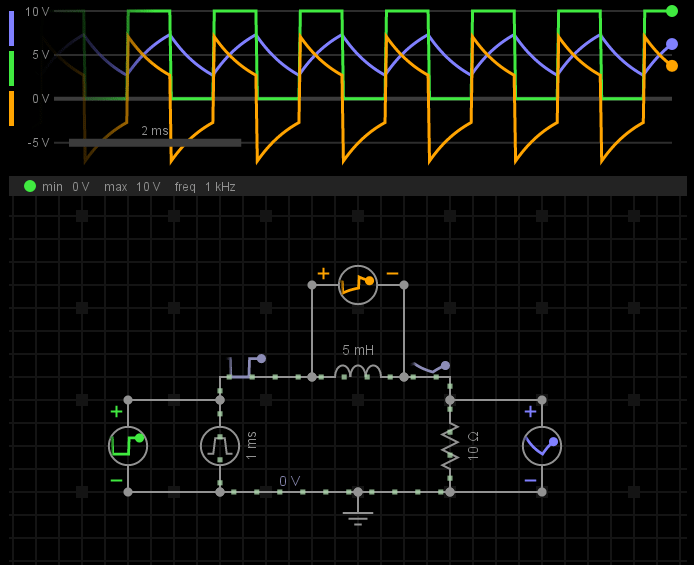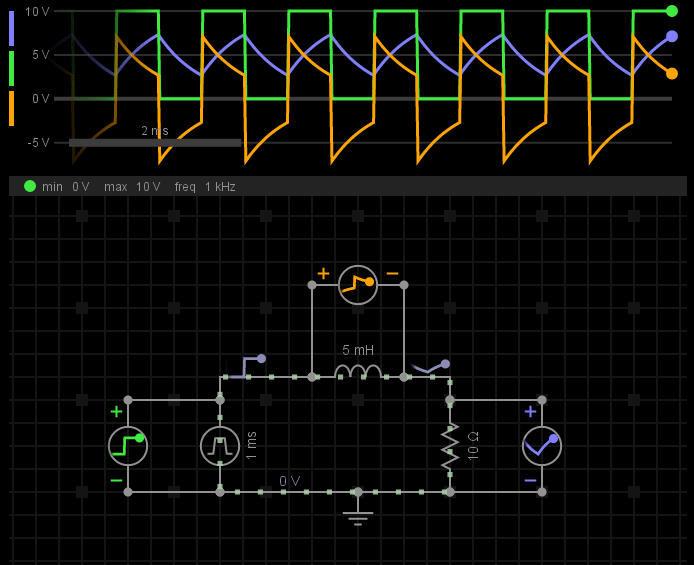
图5-电感感抗随频率的变化
在这个电路中,随着频率的升高,意味着电感阻抗变大了,于是电感上可以分配到更多的电压,而电阻上分配的电压变少了。从另一个角度来说,如果电阻是负载,这难道不是一个降压电路吗?
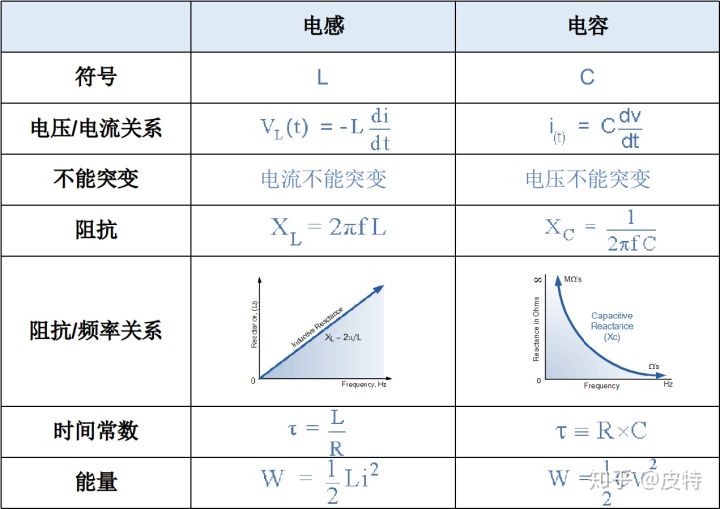
五、电感与电容对比(公式篇)
我们来列举一下电感和电容的对比,帮助大家记忆: